6DOF (Quaternion)
Implement quaternion representation of six-degrees-of-freedom equations of motion with respect to body axes
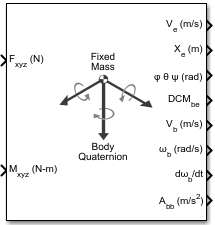
Libraries:
Aerospace Blockset /
Equations of Motion /
6DOF
Description
The 6DOF (Quaternion) block implements quaternion representation of six-degrees-of-freedom equations of motion with respect to body axes. For a description of the coordinate system and the translational dynamics, see the block description for the 6DOF (Euler Angles) block.
For more information on the integration of the rate of change of the quaternion vector, see Algorithms.
Limitations
The block assumes that the applied forces act at the center of gravity of the body, and that the mass and inertia are constant.
Ports
Input
Fxyz(N) — Applied forces
three-element vector
Applied forces, specified as a three-element vector in body-fixed axes. For more information on the frame, see Body Coordinates.
Data Types: double
Mxyz(N-m) — Applied moments
three-element vector
Applied moments, specified as a three-element vector in body-fixed axes. For more information on the frame, see Body Coordinates.
Data Types: double
Output
Ve
— Velocity in flat Earth reference frame
three-element vector
Velocity in the flat Earth reference frame, returned as a three-element vector.
Data Types: double
Xe — Position in flat Earth reference frame
three-element vector
Position in the flat Earth reference frame, returned as a three-element vector.
Data Types: double
φ θ ψ (rad) — Euler rotation angles
three-element vector
Euler rotation angles [roll, pitch, yaw] defining an intrinsic
x-y-z rotation,
as a three-element vector, in radians. Yaw, pitch, and roll angles are
applied using the
z-y-x rotation
sequence, such as angle2dcm(yaw,pitch,roll,"ZYX").
Data Types: double
DCMbe — Coordinate transformation
3-by-3 matrix
Coordinate transformation from flat Earth axes to body-fixed axes, returned as a 3-by-3 matrix.
Data Types: double
Vb — Velocity in the body-fixed frame
three-element vector
Velocity in the body-fixed frame, returned as a three-element vector.
Data Types: double
ωb (rad/s) — Angular rates in body-fixed axes
three-element vector
Angular rates in body-fixed axes, returned as a three-element vector, in radians per second.
Data Types: double
dωb/dt — Angular accelerations
three-element vector
Angular accelerations in body-fixed axes, returned as a three-element vector, in radians per second squared.
Data Types: double
Abb — Accelerations in body-fixed axes
three-element vector
Accelerations in body-fixed axes with respect to body frame, returned as a three-element vector.
Data Types: double
Abe — Accelerations with respect to inertial frame
three-element vector
Accelerations in body-fixed axes with respect to inertial frame (flat Earth), returned as a three-element vector. You typically connect this signal to the accelerometer.
Dependencies
This port appears only when the Include inertial acceleration check box is selected.
Data Types: double
Parameters
Main
Units — Input and output units
Metric (MKS) (default) | English (Velocity in ft/s) | English (Velocity in kts)
Input and output units, specified as Metric (MKS), English (Velocity in ft/s), or English (Velocity in kts).
| Units | Forces | Moment | Acceleration | Velocity | Position | Mass | Inertia |
|---|---|---|---|---|---|---|---|
Metric (MKS) | Newton | Newton-meter | Meters per second squared | Meters per second | Meters | Kilogram | Kilogram meter squared |
English (Velocity in ft/s) | Pound | Foot-pound | Feet per second squared | Feet per second | Feet | Slug | Slug foot squared |
English (Velocity in kts) | Pound | Foot-pound | Feet per second squared | Knots | Feet | Slug | Slug foot squared |
Programmatic Use
Block Parameter:
units |
| Type: character vector |
Values: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts) |
Default: Metric (MKS) |
Mass Type — Mass type
Fixed (default) | Simple Variable | Custom Variable
Mass type, specified according to the following table.
| Mass Type | Description | Default for |
|---|---|---|
Fixed | Mass is constant throughout the simulation. | |
Simple Variable | Mass and inertia vary linearly as a function of mass rate. | |
Custom Variable | Mass and inertia variations are customizable. |
The Simple Variable selection conforms to the previously described equations of motion.
Programmatic Use
Block Parameter: mtype |
| Type: character vector |
Values: Fixed | Simple Variable | Custom Variable |
Default: Simple Variable |
Representation — Equations of motion representation
Quaternion (default) | Euler Angles
Equations of motion representation, specified according to the following table.
| Representation | Description |
|---|---|
| Use Euler angles within equations of motion. |
| Use quaternions within equations of motion. |
The Quaternion selection conforms to the equations of motion in
Algorithms.
Programmatic Use
Block Parameter:
rep |
| Type: character vector |
Values:
Euler Angles |
Quaternion |
Default:
'Quaternion' |
Initial position in inertial axes [Xe,Ye,Ze] — Position in inertial axes
[0 0 0] (default) | three-element vector
Initial location of the body in the flat Earth reference frame, specified as a three-element vector.
Programmatic Use
Block Parameter: xme_0 |
| Type: character vector |
Values:
'[0 0 0]' | three-element vector |
Default:
'[0 0 0]' |
Initial velocity in body axes [U,v,w] — Velocity in body axes
[0 0 0] (default) | three-element vector
Initial velocity in body axes, specified as a three-element vector, in the body-fixed coordinate frame.
Programmatic Use
Block Parameter: Vm_0 |
| Type: character vector |
Values:
'[0 0 0]' | three-element
vector |
Default:
'[0 0 0]' |
Initial Euler orientation [roll, pitch, yaw] — Initial Euler orientation
[0 0 0] (default) | three-element vector
Initial Euler orientation angles [roll, pitch, yaw], specified as a three-element vector, in radians. Euler rotation angles are those between the body and north-east-down (NED) coordinate systems.
Programmatic Use
Block Parameter: eul_0 |
| Type: character vector |
Values:
'[0 0 0]' | three-element vector |
Default:
'[0 0 0]' |
Initial body rotation rates [p,q,r] — Initial body rotation
[0 0 0] (default) | three-element vector
Initial body-fixed angular rates with respect to the NED frame, specified as a three-element vector, in radians per second.
Programmatic Use
Block Parameter: pm_0 |
| Type: character vector |
Values:
'[0 0 0]' | three-element
vector |
Default:
'[0 0 0]' |
Initial mass — Initial mass
1.0 (default) | scalar
Initial mass of the rigid body, specified as a double scalar.
Programmatic Use
Block Parameter: mass_0 |
| Type: character vector |
Values:
'1.0' | double scalar |
Default:
'1.0' |
Inertia — Inertia
eye(3) (default) | scalar
Inertia of the body, specified as a double scalar.
Dependencies
To enable this parameter, set Mass type to
Fixed.
Programmatic Use
Block Parameter: inertia |
| Type: character vector |
Values:
eye(3) | double scalar |
Default: eye(3) |
Gain for quaternion normalization — Gain
1.0 (default) | scalar
Gain to maintain the norm of the quaternion vector equal to 1.0, specified as a double scalar.
Programmatic Use
Block Parameter: k_quat |
| Type: character vector |
Values:
1.0 | double scalar |
Default: 1.0 |
Include inertial acceleration — Include inertial acceleration port
off (default) | on
Select this check box to add an inertial acceleration port.
Dependencies
To enable the Ab ff port, select this parameter.
Programmatic Use
Block Parameter: abi_flag |
| Type: character vector |
Values:
'off' | 'on' |
Default: off |
State Attributes
Assign a unique name to each state. You can use state names instead of block paths during linearization.
To assign a name to a single state, enter a unique name between quotes, for example,
'velocity'.To assign names to multiple states, enter a comma-separated list surrounded by braces, for example,
{'a', 'b', 'c'}. Each name must be unique.If a parameter is empty (
' '), no name is assigned.The state names apply only to the selected block with the name parameter.
The number of states must divide evenly among the number of state names.
You can specify fewer names than states, but you cannot specify more names than states.
For example, you can specify two names in a system with four states. The first name applies to the first two states and the second name to the last two states.
To assign state names with a variable in the MATLAB® workspace, enter the variable without quotes. A variable can be a character vector, cell array, or structure.
Position: e.g., {'Xe', 'Ye', 'Ze'} — Position state name
'' (default) | comma-separated list surrounded by braces
Position state names, specified as a comma-separated list surrounded by braces.
Programmatic Use
Block Parameter: xme_statename |
| Type: character vector |
Values:
'' | comma-separated list surrounded by braces |
Default: '' |
Velocity: e.g., {'U', 'v', 'w'} — Velocity state name
'' (default) | comma-separated list surrounded by braces
Velocity state names, specified as comma-separated list surrounded by braces.
Programmatic Use
Block Parameter: Vm_statename |
| Type: character vector |
Values:
'' | comma-separated list surrounded by braces |
Default: '' |
Quaternion vector: e.g., {'qr', 'qi', 'qj', 'qk'} — Quaternion vector state name
'' (default) | comma-separated list surrounded by braces
Quaternion vector state names, specified as a comma-separated list surrounded by braces.
Programmatic Use
Block Parameter: quat_statename |
| Type: character vector |
Values:
'' | comma-separated list surrounded by braces |
Default: '' |
Body rotation rates: e.g., {'p', 'q', 'r'} — Body rotation state names
'' (default) | comma-separated list surrounded by braces
Body rotation rate state names, specified comma-separated list surrounded by braces.
Programmatic Use
Block Parameter:
pm_statename |
| Type: character vector |
Values:
'' | comma-separated list surrounded by braces |
Default:
'' |
Algorithms
The integration of the rate of change of the quaternion vector is given below. The gain K drives the norm of the quaternion state vector to 1.0 should become nonzero. You must choose the value of this gain with care, because a large value improves the decay rate of the error in the norm, but also slows the simulation because fast dynamics are introduced. An error in the magnitude in one element of the quaternion vector is spread equally among all the elements, potentially increasing the error in the state vector.
Aerospace Blockset™ uses quaternions that are defined using the scalar-first convention.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2006a
See Also
6DOF (Euler Angles) | 6DOF ECEF (Quaternion) | 6DOF Wind (Quaternion) | 6DOF Wind (Wind Angles) | Custom Variable Mass 6DOF (Euler Angles) | Custom Variable Mass 6DOF (Quaternion) | Custom Variable Mass 6DOF ECEF (Quaternion) | Custom Variable Mass 6DOF Wind (Quaternion) | Custom Variable Mass 6DOF Wind (Wind Angles) | Simple Variable Mass 6DOF (Euler Angles) | Simple Variable Mass 6DOF (Quaternion) | Simple Variable Mass 6DOF ECEF (Quaternion) | Simple Variable Mass 6DOF Wind (Quaternion) | Simple Variable Mass 6DOF Wind (Wind Angles)
MATLAB 命令
您点击的链接对应于以下 MATLAB 命令:
请在 MATLAB 命令行窗口中直接输入以执行命令。Web 浏览器不支持 MATLAB 命令。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)