gradient
数值梯度
语法
说明
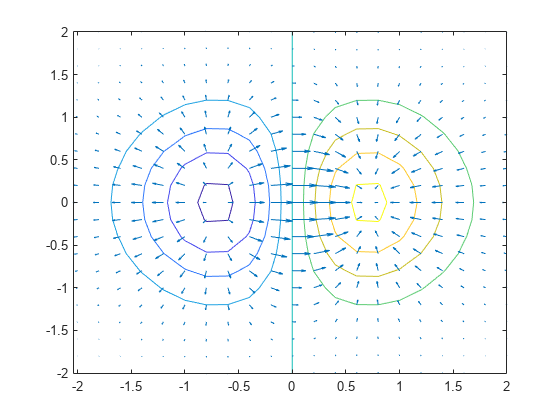
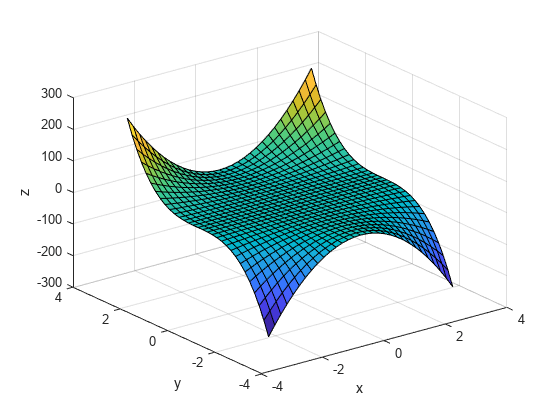
示例
输入参数
输出参量
详细信息
提示
使用
diff或自定义算法计算多个数值导数,而不是多次调用gradient。
算法
gradient 计算内部数据点的中心差分。例如,考虑一个包含单位间距数据的矩阵 A,它具有水平梯度 G = gradient(A)。内部梯度值 G(:,j) 为:
G(:,j) = 0.5*(A(:,j+1) - A(:,j-1));
下标 j 在 2 和 N-1 之间变化,其中 N = size(A,2)。
gradient 使用单侧差分计算沿矩阵边的值:
G(:,1) = A(:,2) - A(:,1); G(:,N) = A(:,N) - A(:,N-1);
如果您指定了点间距,gradient 会对差分进行相应的缩放。如果您指定了两个或更多个输出,该函数还可以按类似方式计算沿其他维度的差分。与 diff 函数不同,gradient 返回与输入具有相同数量元素的数组。
扩展功能
版本历史记录
在 R2006a 之前推出