polyfit
多项式曲线拟合
说明
示例
将多项式与三角函数拟合
在区间 [0,4*pi] 中沿正弦曲线生成 10 个等间距的点。
x = linspace(0,4*pi,10); y = sin(x);
使用 polyfit 将一个 7 次多项式与这些点拟合。
p = polyfit(x,y,7);
在更精细的网格上计算多项式并绘制结果图。
x1 = linspace(0,4*pi); y1 = polyval(p,x1); figure plot(x,y,'o') hold on plot(x1,y1) hold off
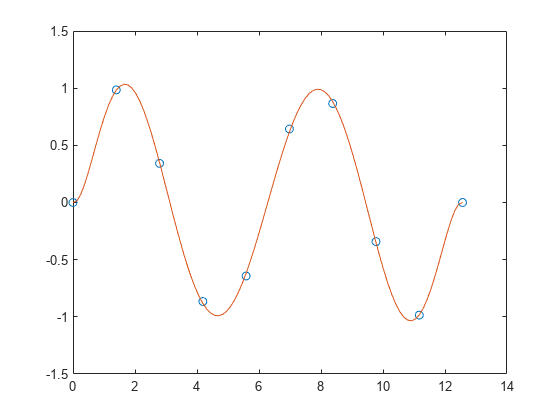
将多项式与点集拟合
创建一个由区间 [0,1] 中的 5 个等间距点组成的向量,并计算这些点处的 。
x = linspace(0,1,5); y = 1./(1+x);
将 4 次多项式与 5 个点拟合。通常,对于 n 个点,可以拟合 n-1 次多项式以便完全通过这些点。
p = polyfit(x,y,4);
在由 0 和 2 之间的点组成的更精细网格上计算原始函数和多项式拟合。
x1 = linspace(0,2); y1 = 1./(1+x1); f1 = polyval(p,x1);
在更大的区间 [0,2] 中绘制函数值和多项式拟合,其中包含用于获取以圆形突出显示的多项式拟合的点。多项式拟合在原始 [0,1] 区间中的效果较好,但在该区间外部很快与拟合函数出现差异。
figure plot(x,y,'o') hold on plot(x1,y1) plot(x1,f1,'r--') legend('y','y1','f1')
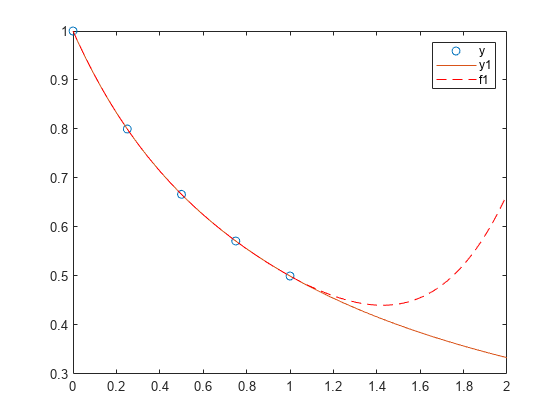
对误差函数进行多项式拟合
首先生成 x 点的向量,在区间 [0,2.5] 内等间距分布;然后计算这些点处的 erf(x)。
x = (0:0.1:2.5)'; y = erf(x);
确定 6 次逼近多项式的系数。
p = polyfit(x,y,6)
p = 1×7
0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004
为了查看拟合情况如何,在各数据点处计算多项式,并生成说明数据、拟合和误差的一个表。
f = polyval(p,x); T = table(x,y,f,y-f,'VariableNames',{'X','Y','Fit','FitError'})
T=26×4 table
X Y Fit FitError
___ _______ __________ ___________
0 0 0.00044117 -0.00044117
0.1 0.11246 0.11185 0.00060836
0.2 0.2227 0.22231 0.00039189
0.3 0.32863 0.32872 -9.7429e-05
0.4 0.42839 0.4288 -0.00040661
0.5 0.5205 0.52093 -0.00042568
0.6 0.60386 0.60408 -0.00022824
0.7 0.6778 0.67775 4.6383e-05
0.8 0.7421 0.74183 0.00026992
0.9 0.79691 0.79654 0.00036515
1 0.8427 0.84238 0.0003164
1.1 0.88021 0.88005 0.00015948
1.2 0.91031 0.91035 -3.9919e-05
1.3 0.93401 0.93422 -0.000211
1.4 0.95229 0.95258 -0.00029933
1.5 0.96611 0.96639 -0.00028097
⋮
在该区间中,插值与实际值非常符合。创建一个绘图,以显示在该区间以外,外插值与实际数据值如何快速偏离。
x1 = (0:0.1:5)'; y1 = erf(x1); f1 = polyval(p,x1); figure plot(x,y,'o') hold on plot(x1,y1,'-') plot(x1,f1,'r--') axis([0 5 0 2]) hold off
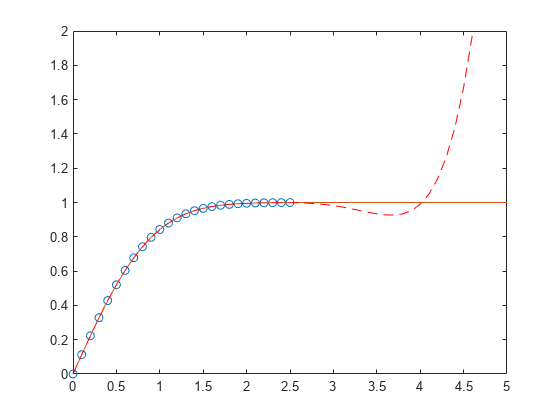
使用中心化和缩放改善数值属性
创建一个由 1750 - 2000 年的人口数据组成的表,并绘制数据点。
year = (1750:25:2000)'; pop = 1e6*[791 856 978 1050 1262 1544 1650 2532 6122 8170 11560]'; T = table(year, pop)
T=11×2 table
year pop
____ _________
1750 7.91e+08
1775 8.56e+08
1800 9.78e+08
1825 1.05e+09
1850 1.262e+09
1875 1.544e+09
1900 1.65e+09
1925 2.532e+09
1950 6.122e+09
1975 8.17e+09
2000 1.156e+10
plot(year,pop,'o')
使用带三个输入的 polyfit 拟合一个使用中心化和缩放的 5 次多项式,这将改善问题的数值属性。polyfit 将 year 中的数据以 0 为进行中心化,并缩放为具有标准差 1,这可避免在拟合计算中出现病态的范德蒙矩阵。
[p,~,mu] = polyfit(T.year, T.pop, 5);
使用带四个输入的 polyval,根据缩放后的年份 (year-mu(1))/mu(2) 计算 p。绘制结果对原始年份的图。
f = polyval(p,year,[],mu); hold on plot(year,f) hold off
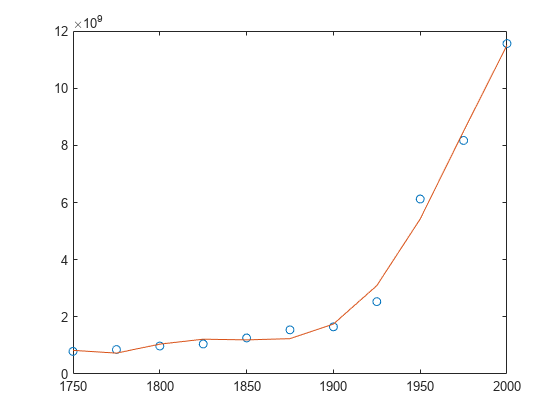
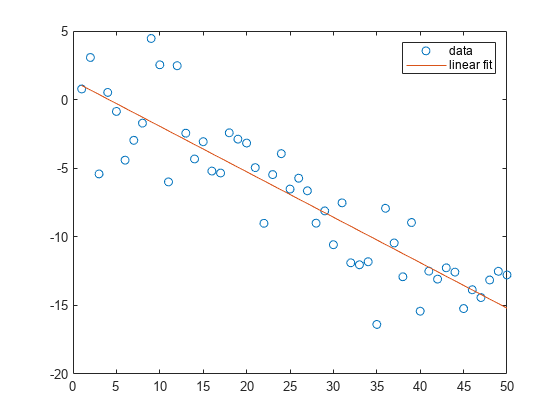
简单线性回归
将一个简单线性回归模型与一组离散二维数据点拟合。
创建几个由样本数据点 (x,y) 组成的向量。对数据进行一次多项式拟合。
x = 1:50; y = -0.3*x + 2*randn(1,50); p = polyfit(x,y,1);
计算在 x 中的点处拟合的多项式 p。用这些数据绘制得到的线性回归模型。
f = polyval(p,x); plot(x,y,'o',x,f,'-') legend('data','linear fit')
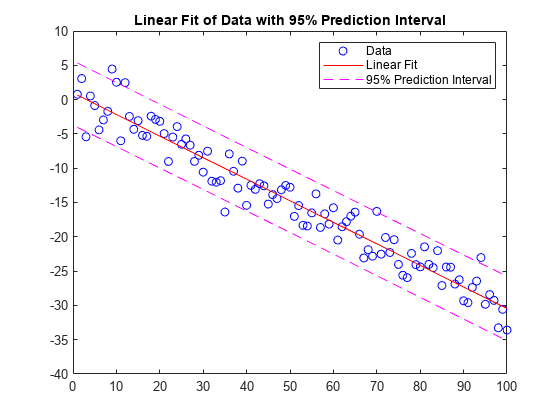
具有误差估计值的线性回归
将一个线性模型拟合到一组数据点并绘制结果,其中包含预测区间为 95% 的估计值。
创建几个由样本数据点 (x,y) 组成的向量。使用 polyfit 对数据进行一次多项式拟合。指定两个输出以返回线性拟合的系数以及误差估计结构体。
x = 1:100; y = -0.3*x + 2*randn(1,100); [p,S] = polyfit(x,y,1);
计算以 p 为系数的一次多项式在 x 中各点处的拟合值。将误差估计结构体指定为第三个输入,以便 polyval 计算标准误差的估计值。标准误差估计值在 delta 中返回。
[y_fit,delta] = polyval(p,x,S);
绘制原始数据、线性拟合和 95% 预测区间 。
plot(x,y,'bo') hold on plot(x,y_fit,'r-') plot(x,y_fit+2*delta,'m--',x,y_fit-2*delta,'m--') title('Linear Fit of Data with 95% Prediction Interval') legend('Data','Linear Fit','95% Prediction Interval')
输入参数
x — 查询点
向量
查询点,指定为一个向量。x 中的点对应于 y 中包含的拟合函数值。如果 x 不是向量,则 polyfit 将其转换为列向量 x(:)。
x 具有重复(或接近重复)的点或者如果 x 可能需要中心化和缩放时的警告消息结果。
数据类型: single | double
复数支持: 是
y — 查询点位置的拟合值
向量
查询点位置的拟合值,指定为向量。y 中的值对应于 x 中包含的查询点。如果 y 不是向量,则 polyfit 将其转换为列向量 y(:)。
数据类型: single | double
复数支持: 是
n — 多项式拟合的次数
正整数标量
多项式拟合的次数,指定为正整数标量。n 指定 p 中最左侧系数的多项式幂。
输出参数
p — 最小二乘拟合多项式系数
向量
最小二乘拟合多项式系数,以向量的形式返回。p 的长度为 n+1,包含按降幂排列的多项式系数,最高幂为 n。如果 x 或 y 包含 NaN 值且 n < length(x),则 p 的所有元素均为 NaN。如果您指定三个输出参数来中心化和缩放数据,则与未对数据进行中心化和缩放时相比,polyfit 在 p 中返回的系数会有所不同。
使用 polyval 计算 p 在查询点处的解。
S — 误差估计结构体
结构体
误差估计结构体。此可选输出结构体主要用作 polyval 函数的输入,以获取误差估计值。S 包含以下字段:
| 字段 | 描述 |
|---|---|
R | 范德蒙矩阵 x 的 QR 分解的三角 R 因子(可能经过置换) |
df | 自由度 |
normr | 残差的范数 |
如果 y 中的数据是随机的,则 p 的估计协方差矩阵是 (Rinv*Rinv')*normr^2/df,其中 Rinv 是 R 的逆矩阵。
如果 y 中数据的误差呈独立正态分布,并具有常量方差,则 [y,delta] = polyval(...) 可生成至少包含 50% 的预测值的误差边界。即 y ± delta 至少包含 50% 对 x 处的未来观测值的预测值。
mu — 中心化值和缩放值
二元素向量
中心化值和缩放值,以二元素向量形式返回。mu(1) 为 mean(x),mu(2) 为 std(x)。这些值以单位标准差将 x 中的查询点的中心置于零值处。
使用 mu 作为 polyval 的第四个输入以计算 p 在缩放点 (x - mu(1))/mu(2) 处的解。
局限性
在涉及很多点的问题中,使用
polyfit增加多项式拟合的次数并不总能得到较好的拟合。高次多项式可以在数据点之间振动,导致与数据之间的拟合较差。在这些情况下,可使用低次多项式拟合(点之间倾向于更平滑)或不同的方法,具体取决于该问题。多项式在本质上是无边界的振荡函数。所以,它们并不非常适合外插有界的数据或单调(递增或递减)的数据。
算法
polyfit 使用 x 构造具有 n+1 列和 m = length(x) 行的范德蒙矩阵 V 并生成线性系统
其中 polyfit 使用 p = V\y 求解。由于范德蒙矩阵中的列是向量 x 的幂,因此条件数 V 对于高阶拟合来说通常较大,生成一个奇异系数矩阵。在这些情况下,中心化和缩放可改善系统的数值属性以产生更可靠的拟合。
扩展功能
tall 数组
对行数太多而无法放入内存的数组进行计算。
C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。
基于线程的环境
使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。
此函数完全支持基于线程的环境。有关详细信息,请参阅在基于线程的环境中运行 MATLAB 函数。
GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。
此函数完全支持 GPU 数组。有关详细信息,请参阅Run MATLAB Functions on a GPU (Parallel Computing Toolbox)。
分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。
此函数完全支持分布式数组。有关详细信息,请参阅Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox)。
版本历史记录
在 R2006a 之前推出
MATLAB 命令
您点击的链接对应于以下 MATLAB 命令:
请在 MATLAB 命令行窗口中直接输入以执行命令。Web 浏览器不支持 MATLAB 命令。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)