偏最小二乘回归和主成分回归

打开实时脚本

此示例说明如何应用偏最小二乘回归 (PLSR) 和主成分回归 (PCR)，并研究这两种方法的有效性。当存在大量预测变量并且它们高度相关甚至共线时，PLSR 和 PCR 都可以作为建模响应变量的方法。这两种方法都将新的预测变量（称为成分）构建为原始预测变量的线性组合，但它们构建这些成分的方式不同。PCR 创建成分来解释在预测变量中观察到的变异性，而根本不考虑响应变量。而 PLSR 会考虑响应变量，因此常使模型能够拟合具有更少成分的响应变量。从实际应用上来说，这能否最终转化为更简约的模型要视情况而定。

加载数据

加载包括 60 个汽油样本的 401 个波长的光频谱强度及其辛烷值的数据集。这些数据在以下文献中有详细描述：Kalivas, John H., "Two Data Sets of Near Infrared Spectra," Chemometrics and Intelligent Laboratory Systems, v.37 (1997) pp.255-259。

load spectra
whos NIR octane

  Name         Size              Bytes  Class     Attributes

  NIR         60x401            192480  double              
  octane      60x1                 480  double

[dummy,h] = sort(octane);
oldorder = get(gcf,'DefaultAxesColorOrder');
set(gcf,'DefaultAxesColorOrder',jet(60));
plot3(repmat(1:401,60,1)',repmat(octane(h),1,401)',NIR(h,:)');
set(gcf,'DefaultAxesColorOrder',oldorder);
xlabel('Wavelength Index'); ylabel('Octane'); axis('tight');
grid on

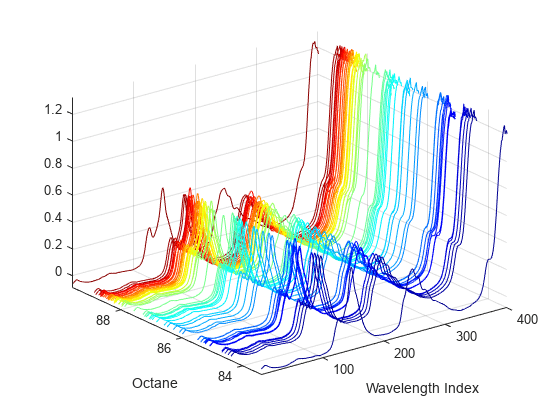
使用两个成分拟合数据

使用 plsregress 函数来拟合一个具有十个 PLS 成分和一个响应变量的 PLSR 模型。

X = NIR;
y = octane;
[n,p] = size(X);
[Xloadings,Yloadings,Xscores,Yscores,betaPLS10,PLSPctVar] = plsregress(...
	X,y,10);

十个成分可能超出充分拟合数据所需要的成分数量，但可以根据此拟合的诊断来选择具有更少成分的简单模型。例如，选择成分数量的一种快速方法是将响应变量中解释的方差百分比绘制为成分数量的函数。

plot(1:10,cumsum(100*PLSPctVar(2,:)),'-bo');
xlabel('Number of PLS components');
ylabel('Percent Variance Explained in Y');

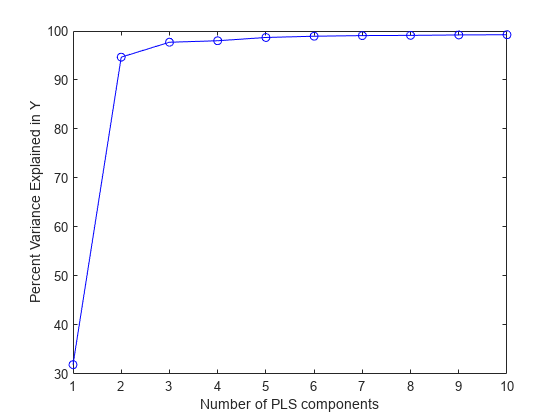
在实际应用中，选择成分数量时可能需要更加谨慎。例如交叉验证就是一种广泛使用的方法，本示例稍后将进行说明。就目前来说，上图显示具有两个成分的 PLSR 即能解释观测的 y 中的大部分方差。计算双成分模型的拟合响应值。

[Xloadings,Yloadings,Xscores,Yscores,betaPLS] = plsregress(X,y,2);
yfitPLS = [ones(n,1) X]*betaPLS;

接下来，拟合具有两个主成分的 PCR 模型。第一步是使用 pca 函数对 X 执行主成分分析，并保留两个主成分。然后，PCR 就只是响应变量对这两个成分的线性回归。当不同变量的取值范围有很大差异时，通常应该先按照变量的标准差来归一化每个变量，但在本例中并没有这样做。

[PCALoadings,PCAScores,PCAVar] = pca(X,'Economy',false);
betaPCR = regress(y-mean(y), PCAScores(:,1:2));

为了更易于对比原始频谱数据解释 PCR 结果，对原始未中心化变量的回归系数进行转换。

betaPCR = PCALoadings(:,1:2)*betaPCR;
betaPCR = [mean(y) - mean(X)*betaPCR; betaPCR];
yfitPCR = [ones(n,1) X]*betaPCR;

绘制 PLSR 和 PCR 两种方法的拟合响应值对观察响应值的图。

plot(y,yfitPLS,'bo',y,yfitPCR,'r^');
xlabel('Observed Response');
ylabel('Fitted Response');
legend({'PLSR with 2 Components' 'PCR with 2 Components'},  ...
	'location','NW');

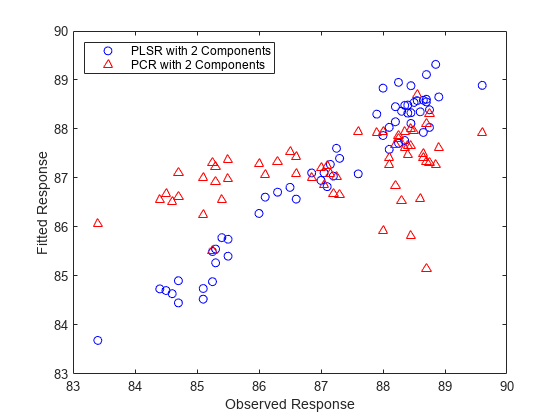
上图中的比较从某种意义上说并不合理 - 成分数量（两个）是通过观察具有两个成分的 PLSR 模型预测响应变量的效果来选择的，而对于 PCR 模型来说，并无充分理由将其成分数量限制为与 PLSR 一致。但是，在成分数量相同的情况下，PLSR 拟合 y 的效果更好。事实上，观察上图中拟合值的水平散点图可以看出，两个成分的 PCR 并不比使用常量模型更好。两种回归的 R 方值证实了这一点。

TSS = sum((y-mean(y)).^2);
RSS_PLS = sum((y-yfitPLS).^2);
rsquaredPLS = 1 - RSS_PLS/TSS

rsquaredPLS = 0.9466

RSS_PCR = sum((y-yfitPCR).^2);
rsquaredPCR = 1 - RSS_PCR/TSS

rsquaredPCR = 0.1962

另一种比较两个模型的预测能力的方法是绘制两种情况下响应变量对两个预测变量的图。

plot3(Xscores(:,1),Xscores(:,2),y-mean(y),'bo');
legend('PLSR');
grid on; view(-30,30);

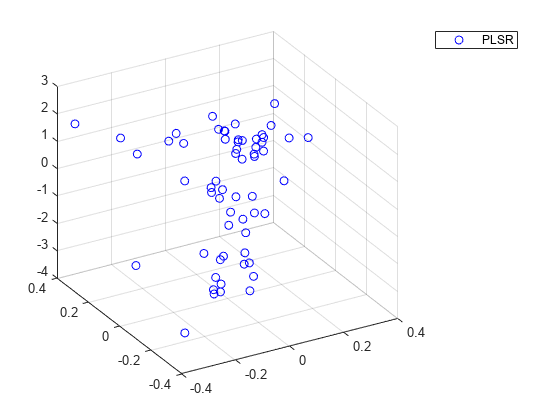
虽然可能需要交互旋转图形才能明显地看出分布情况，但上面的 PLSR 图还是显示出点几乎都散布在一个平面上。而下面的 PCR 图显示一片点云，几乎看不出线性关系。

plot3(PCAScores(:,1),PCAScores(:,2),y-mean(y),'r^');
legend('PCR');
grid on; view(-30,30);

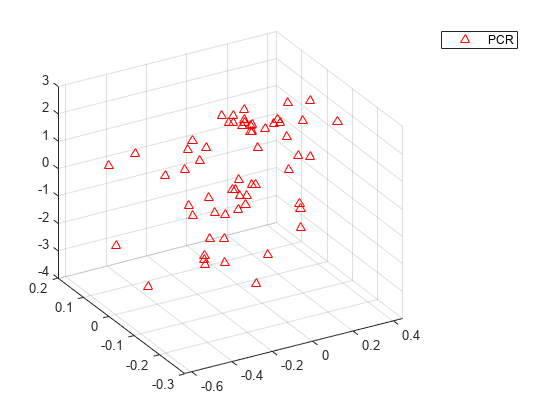
请注意，虽然这两个 PLS 成分对 y 观测值而言预测效果较好，但下图显示，相比 PCR 所用的前两个主成分，这两个 PLS 成分解释的 X 观测值方差比例较少。

plot(1:10,100*cumsum(PLSPctVar(1,:)),'b-o',1:10,  ...
	100*cumsum(PCAVar(1:10))/sum(PCAVar(1:10)),'r-^');
xlabel('Number of Principal Components');
ylabel('Percent Variance Explained in X');
legend({'PLSR' 'PCR'},'location','SE');

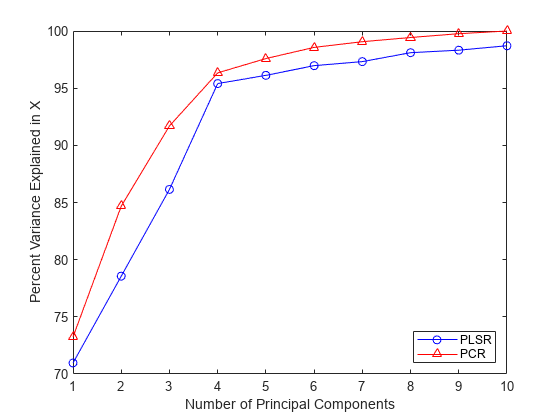
PCR 曲线更均匀的事实说明了为什么具有两个成分的 PCR 在拟合 y 方面比 PLSR 差。PCR 构造成分是为了最好地解释 X，因此前两个成分忽略了数据中对拟合观察到的 y 重要的信息。

使用更多成分拟合数据

在 PCR 中添加更多成分后，它必然可以更好地拟合原始数据 y，因为 X 中的大多数重要预测信息都会在某个点出现在主成分中。例如，下图显示，使用十个成分时，两种方法的残差差异远小于使用两个成分时。

yfitPLS10 = [ones(n,1) X]*betaPLS10;
betaPCR10 = regress(y-mean(y), PCAScores(:,1:10));
betaPCR10 = PCALoadings(:,1:10)*betaPCR10;
betaPCR10 = [mean(y) - mean(X)*betaPCR10; betaPCR10];
yfitPCR10 = [ones(n,1) X]*betaPCR10;
plot(y,yfitPLS10,'bo',y,yfitPCR10,'r^');
xlabel('Observed Response');
ylabel('Fitted Response');
legend({'PLSR with 10 components' 'PCR with 10 Components'},  ...
	'location','NW');

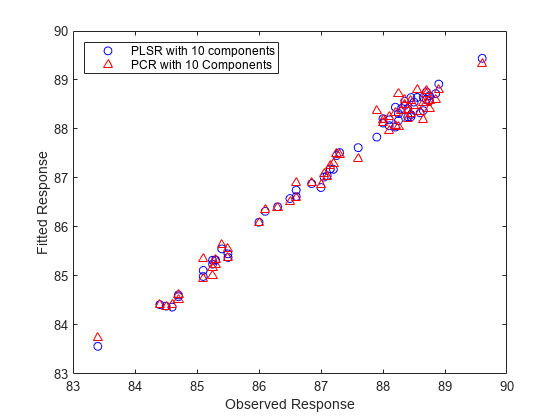
虽然 PLSR 拟合的准确度稍高一点，不过，两个模型都比较准确地拟合了 y。但是，十个成分对任一模型来说仍然是任意选择的数字。

通过交叉验证选择成分数量

在预测未来观测值对预测变量的响应时，选择适当数量的成分以最大程度减少预期误差通常很有用。简单地使用大量成分将能够很好地拟合当前观察到的数据，但这种策略往往会导致过拟合。太好地拟合当前数据会导致模型不能很好地推广到其他数据，并对预期误差给出过度乐观的估计。

交叉验证是统计学上更加合理的成分数量选择方法，不管是在 PLSR 中还是在 PCR 中。它在拟合模型和估计预测误差时使用不同的数据，从而避免过拟合数据。因此，预测误差的估计值不会乐观地偏小。

plsregress 有一个选项可以通过交叉验证来估计均方预测误差 (MSEP)，此处我们使用 10 折交叉验证。

[Xl,Yl,Xs,Ys,beta,pctVar,PLSmsep] = plsregress(X,y,10,'CV',10);

对于 PCR，将 crossval 与一个简单的函数（计算 PCR 的平方误差之和）相结合，可以估计 MSEP，在此同样使用 10 折交叉验证。

PCRmsep = sum(crossval(@pcrsse,X,y,'KFold',10),1) / n;

PLSR 的 MSEP 曲线表明，两个或三个成分的效果已经足够好。另一方面，PCR 需要四个成分才能获得同样的预测准确度。

plot(0:10,PLSmsep(2,:),'b-o',0:10,PCRmsep,'r-^');
xlabel('Number of components');
ylabel('Estimated Mean Squared Prediction Error');
legend({'PLSR' 'PCR'},'location','NE');

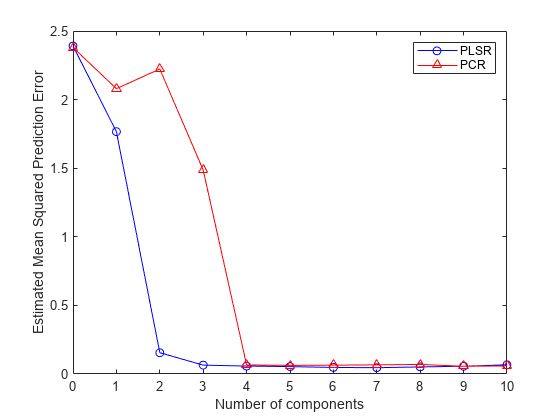
事实上，PCR 中的第二个成分会增加模型的预测误差，表明该成分中包含的预测变量的组合与 y 没有很强的相关性。同样，这是因为 PCR 的构造成分是为了解释 X 而非 y 的变异。

模型精简

因此，如果 PCR 需要四个成分才能获得与具有三个成分的 PLSR 相同的预测精度，是否说明 PLSR 模型更加精简呢？这取决于您考虑的是模型的哪个方面。

PLS 权重是定义 PLS 成分的原始变量的线性组合，即，它们描述 PLSR 中的每个成分依赖原始变量的程度和方向。

[Xl,Yl,Xs,Ys,beta,pctVar,mse,stats] = plsregress(X,y,3);
plot(1:401,stats.W,'-');
xlabel('Variable');
ylabel('PLS Weight');
legend({'1st Component' '2nd Component' '3rd Component'},  ...
	'location','NW');

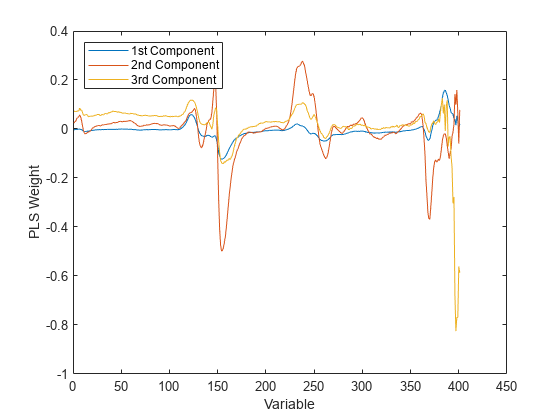
同样，PCA 载重描述 PCR 中的每个成分依赖原始变量的程度。

plot(1:401,PCALoadings(:,1:4),'-');
xlabel('Variable');
ylabel('PCA Loading');
legend({'1st Component' '2nd Component' '3rd Component'  ...
	'4th Component'},'location','NW');

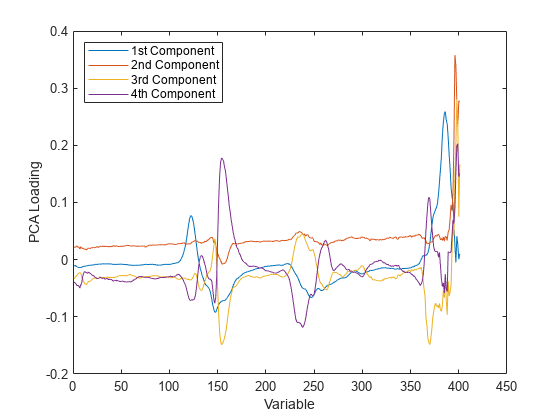
不管对于 PLSR 还是 PCR，都可以通过检查哪些变量的权重最大来为每个成分提供一个具有实际意义的解释。例如，利用这些频谱数据，也许能够从汽油中存在的化合物的角度解释强度波峰，然后观察特定成分的权重，从中选出少数几种化合物。从这个角度来说，成分越少越容易解释，而且因为 PLSR 通常需要更少的成分就能充分地预测响应，所以模型更精简。

另一方面，PLSR 和 PCR 为每个原始预测变量都生成一个回归系数和一个截距。从这个意义上讲，二者都不算精简，因为无论使用多少成分，两个模型都依赖于所有预测变量。再具体一点，对于这些数据，两个模型都需要 401 个频谱强度值才能进行预测。

然而，最终目的可能是将原始变量集缩减为更小但仍能准确预测响应的子集。例如，可以使用 PLS 权重或 PCA 载重只选择对每个成分贡献最大的那些变量。正如前文所示，PCR 模型拟合中的一些成分主要用于描述预测变量的变异，与响应的相关性不强的那些变量可能具有较大的权重。因此，PCR 可能会导致那些对预测不必要的变量被保留下来。

对于本例中使用的数据，PLSR 和 PCR 进行精确预测所需要的成分数量差别不是太大，而且 PLS 权重和 PCA 载重似乎选择了相同的变量。对于其他数据，情况可能并非如此。

另请参阅

pca | plsregress