bessely
Bessel function of the second kind for symbolic expressions
Syntax
Description
bessely( returns the
Bessel function of the second
kind, Yν(z).nu,z)
Examples
Find Bessel Function of Second Kind
Compute the Bessel functions of the second kind for these numbers. Because these numbers are not symbolic objects, you get floating-point results.
[bessely(0, 5), bessely(-1, 2), bessely(1/3, 7/4), bessely(1, 3/2 + 2*i)]
ans = -0.3085 + 0.0000i 0.1070 + 0.0000i 0.2358 + 0.0000i -0.4706 + 1.5873i
Compute the Bessel functions of the second kind for the numbers converted to symbolic
objects. For most symbolic (exact) numbers, bessely returns unresolved
symbolic calls.
[bessely(sym(0), 5), bessely(sym(-1), 2),... bessely(1/3, sym(7/4)), bessely(sym(1), 3/2 + 2*i)]
ans = [ bessely(0, 5), -bessely(1, 2), bessely(1/3, 7/4), bessely(1, 3/2 + 2i)]
For symbolic variables and expressions, bessely also returns
unresolved symbolic calls:
syms x y [bessely(x, y), bessely(1, x^2), bessely(2, x - y), bessely(x^2, x*y)]
ans = [ bessely(x, y), bessely(1, x^2), bessely(2, x - y), bessely(x^2, x*y)]
Solve Bessel Differential Equation for Bessel Functions
Solve this second-order differential equation. The solutions are the Bessel functions of the first and the second kind.
syms nu w(z) dsolve(z^2*diff(w, 2) + z*diff(w) +(z^2 - nu^2)*w == 0)
ans = C2*besselj(nu, z) + C3*bessely(nu, z)
Verify that the Bessel function of the second kind is a valid solution of the Bessel differential equation:
syms nu z isAlways(z^2*diff(bessely(nu, z), z, 2) + z*diff(bessely(nu, z), z)... + (z^2 - nu^2)*bessely(nu, z) == 0)
ans = logical 1
Special Values of Bessel Function of Second Kind
If the first parameter is an odd integer multiplied by 1/2, bessely
rewrites the Bessel functions in terms of elementary functions:
syms x bessely(1/2, x)
ans = -(2^(1/2)*cos(x))/(x^(1/2)*pi^(1/2))
bessely(-1/2, x)
ans = (2^(1/2)*sin(x))/(x^(1/2)*pi^(1/2))
bessely(-3/2, x)
ans = (2^(1/2)*(cos(x) - sin(x)/x))/(x^(1/2)*pi^(1/2))
bessely(5/2, x)
ans = -(2^(1/2)*((3*sin(x))/x + cos(x)*(3/x^2 - 1)))/(x^(1/2)*pi^(1/2))
Differentiate Bessel Functions of Second Kind
Differentiate the expressions involving the Bessel functions of the second kind:
syms x y diff(bessely(1, x)) diff(diff(bessely(0, x^2 + x*y -y^2), x), y)
ans = bessely(0, x) - bessely(1, x)/x ans = - bessely(1, x^2 + x*y - y^2) -... (2*x + y)*(bessely(0, x^2 + x*y - y^2)*(x - 2*y) -... (bessely(1, x^2 + x*y - y^2)*(x - 2*y))/(x^2 + x*y - y^2))
Find Bessel Function for Matrix Input
Call bessely for the matrix A and the value 1/2.
The result is a matrix of the Bessel functions bessely(1/2,
A(i,j)).
syms x A = [-1, pi; x, 0]; bessely(1/2, A)
ans = [ (2^(1/2)*cos(1)*1i)/pi^(1/2), 2^(1/2)/pi] [ -(2^(1/2)*cos(x))/(x^(1/2)*pi^(1/2)), Inf]
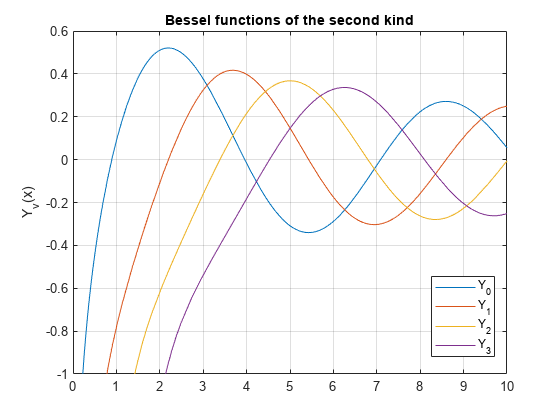
Plot Bessel Functions of Second Kind
Plot the Bessel functions of the second kind for .
syms x y fplot(bessely(0:3,x)) axis([0 10 -1 0.6]) grid on ylabel('Y_v(x)') legend('Y_0','Y_1','Y_2','Y_3', 'Location','Best') title('Bessel functions of the second kind')
Input Arguments
More About
Tips
Calling
besselyfor a number that is not a symbolic object invokes the MATLAB®besselyfunction.At least one input argument must be a scalar or both arguments must be vectors or matrices of the same size. If one input argument is a scalar and the other one is a vector or a matrix,
bessely(nu,z)expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.
References
[1] Olver, F. W. J. “Bessel Functions of Integer Order.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.
[2] Antosiewicz, H. A. “Bessel Functions of Fractional Order.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.
Version History
Introduced in R2014a
