Optimization Toolbox 提供了多个函数,这些函数可在满足约束的同时求出可最小化或最大化目标的参数。该工具箱包含用于线性规划 (LP)、混合整数线性规划 (MILP)、二次规划 (QP)、二阶锥规划 (SOCP)、非线性规划 (NLP)、约束线性最小二乘、非线性最小二乘和非线性方程的求解器。
您可以用函数和矩阵来定义优化问题,也可以通过指定反映底层数学关系的变量表达式来定义。使用目标函数和约束函数自动微分,更快、更准确地求解。
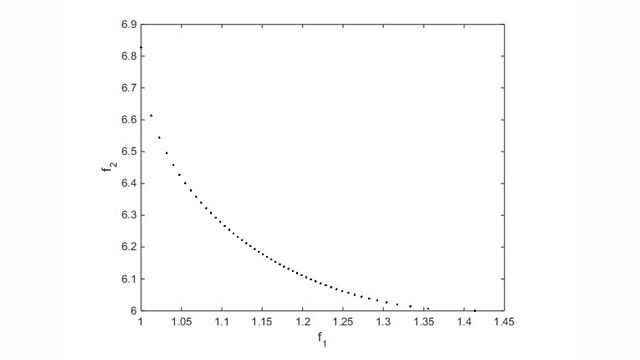
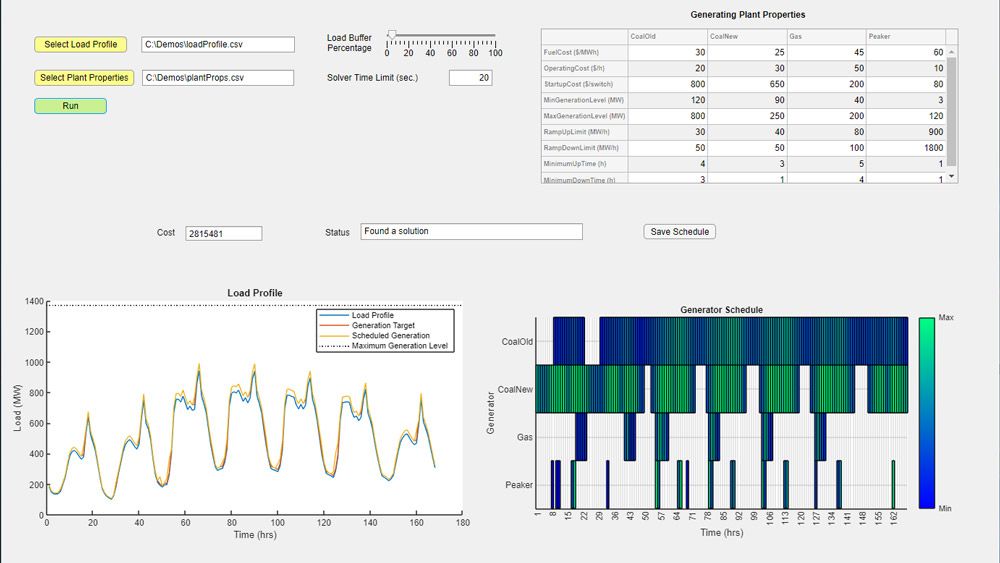
您可以使用该工具箱提供的求解器求连续与离散问题的最优解、执行权衡分析,并将优化方法整合到算法和应用中。该工具箱能够执行设计优化任务,包括参数估计、分量选择和参数调整。它能帮助您在投资组合优化、能源管理和交易以及生产规划等各种应用中求最优解。
定义优化问题
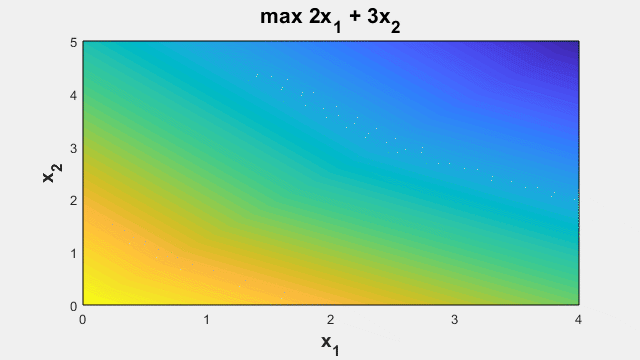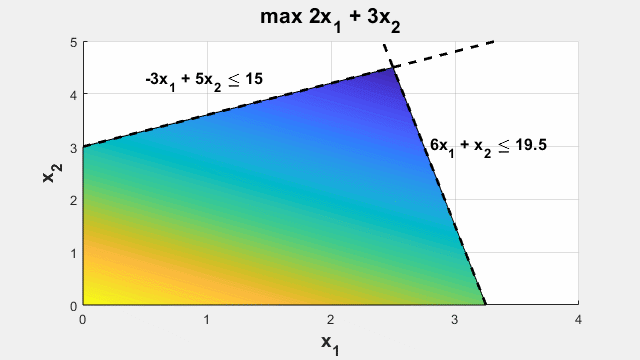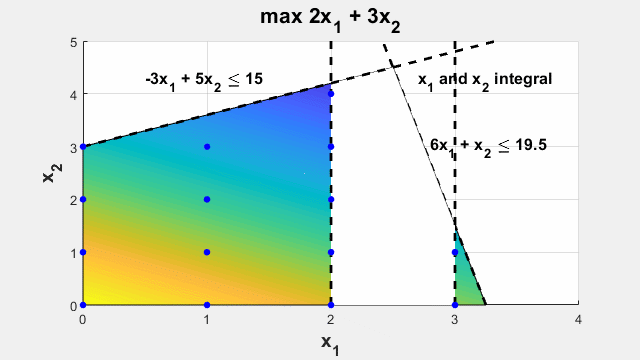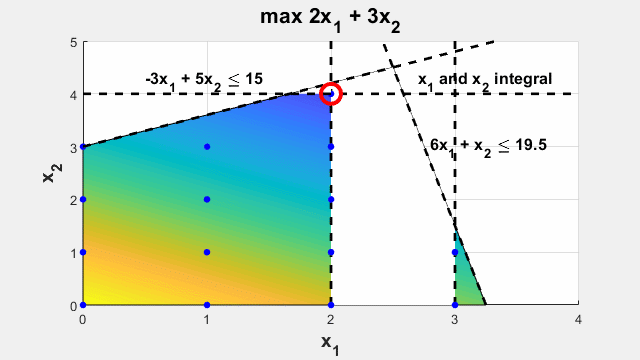
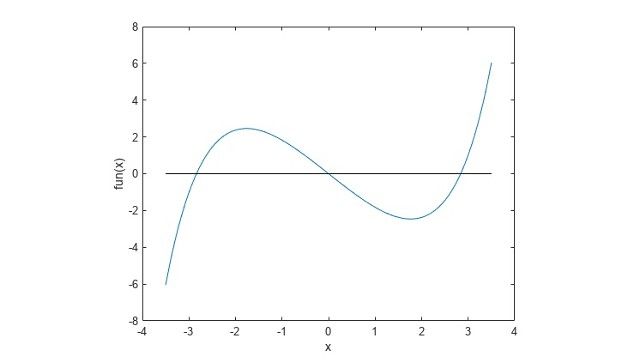
将设计或决策问题建模为优化问题。将设计参数或决策方案设置为优化变量。使用变量来定义要优化的目标函数,并使用约束来限制可能的变量值。
产品资源:
“MATLAB 帮助我们加快了研发和部署,它有着稳健的数值算法、丰富的可视化和分析工具、可靠的优化例程,并支持面向对象编程,还能够配合我们的产品级 Java 应用程序在云端运行。”
Borislav Savkovic,BuildingIQ