Forecasting GDP with a Dynamic Factor Model
By Ángel Cuevas, Spanish Ministry of Industry, Tourism and Trade and Enrique M. Quilis, Spanish Ministry of Economy and Finance
Measuring GDP accurately on a regular basis helps policy makers, economists, and business leaders determine appropriate policies, research direction, and financial strategies. While headline GDP figures are typically reported each quarter, it is helpful for government and business organizations to refer to updated numbers in the weeks between.
At the Ministry of Economy and Finance we have developed a dynamic factor model to estimate and forecast the rate of growth of the Spanish economy in the very short term. This model uses a coincident indicator, or estimated common factor, to forecast GDP by means of a transfer function. The model estimates a common factor underlying 31 economic indicators spanning domestic production, the labor market, and domestic trade flows. It enables us to forecast GDP several times a week, providing a virtually real-time complement to the four quarterly GDP official reports issued each year.
MATLAB® was a natural choice for this work because much of the processing requires matrix operations. Kalman filters simplified the process of estimating the common factor from the economic indicators in a dynamic way.
Selecting the Economic Indicators
With 31 indicators, our model avoids the disadvantages inherent in both larger and smaller models. Models with more than 80 indicators are difficult to interpret, require more work to maintain, and suffer from group effects that can distort the estimation of the common factor. On the other hand, models with fewer than 12 indicators can lack sufficient coverage, omit useful information from excluded indicators, and be more susceptible to the abnormal behavior of a single indicator.
The indicators we use cover a wide range of domestic economic activity, including industrial production, air traffic, cement usage, tourism, energy consumption, transport by railway, housing starts, and employee compensation. We supplement these domestic indicators with external ones, such as imports and exports of goods and services, as well as social security contributors (employment) and other labor-market indicators.
In addition, our model includes qualitative indicators reflecting the level of confidence Spaniards have in their business and household finances. Such indicators are less common in dynamic factor models because they are difficult to integrate with hard data. These so-called soft indicators, however, provide a useful alternative perspective on the economy, and they are promptly available, making them valuable for short-term forecasting.
Preprocessing Data with TRAMO-SEATS
To ensure that our results are not distorted by the presence of seasonal and calendar effects, we remove these effects using seasonal adjustment and time series techniques. At the Bank of Spain, two programs have been developed for the statistical analysis and seasonal adjustment of time series data: TRAMO (Time series Regression with ARIMA errors, Missing values and Outliers) and SEATS (Signal Extraction in ARIMA Time Series).
We invoke the TRAMO-SEATS software from MATLAB to perform seasonal adjustments on the time series indicator data and to verify its integrity. One of our ministry colleagues developed a MATLAB interface to the TRAMO-SEATS software that enables us to execute TRAMO and SEATS applications for time series data directly from MATLAB. After making the seasonal adjustments, we use MATLAB to perform logarithmic and stationary-inducing transformation on the data.
Developing the Dynamic Common Factor Model
The common factor model must consider both static and dynamic interactions among the observed indicators. We use MATLAB to estimate the common factor with principal components. We then use a Kalman filter to introduce dynamics into the model. A complete representation of the dynamic factor model implemented in MATLAB has the form
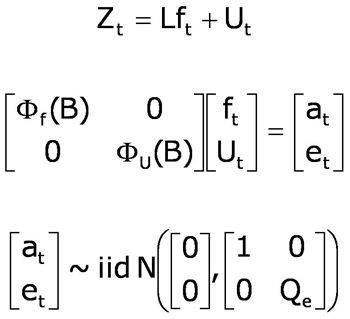
where Zt are observations, ft is the common factor, Ut are idiosyncratic factors, L is a factor loading matrix, Φf(B) is an AR(4) operator, ΦU(B) is a VAR(1) operator with diagonal AR(1) matrix, Qe is a diagonal matrix, and B is the lag (or backshift) operator BZt = Zt-1.
Among the biggest operational challenges that we faced in developing the model was analyzing data from different time periods. We had a complete set of observed data for several indicators over the entire time period (a longitudinal panel), as well as observed data for all indicators over a shorter time period (a cross-section panel). What we lacked was a complete set of observed data for all indicators over the entire time period (Figure 1).

To handle this unbalanced panel, we implemented an iterative process in MATLAB that begins with the estimation of a static factor model by principal components using the longitudinal panel data. Indicators that were excluded from the longitudinal panel are individually regressed using ordinary least squares. We then calculate a new factor from the statically balanced panel and apply a Kalman filter to estimate the missing values. This process, which is repeated until convergence is achieved, is based on an approach outlined by Chang-Jin Kim and Charles R. Nelson [1].
Generating the GDP Forecast
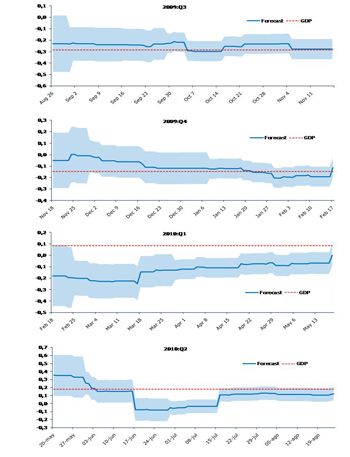
After estimating the common factor using the dynamic factor model, we use a transfer function model to forecast GDP. This model defines a simple and quantitatively consistent relationship between the common factor and the GDP or other macroeconomic aggregates. We use a time series analysis package to derive the parameters of the transfer function and then implement it using MATLAB. We check the specification of the transfer function with the results of a bivariate vector autoregressive and moving average (VARMA) model. Finally, we use the MATLAB filter function to forecast the current quarter GDP based on the common factor and the transfer function. Figure 2 shows the relation of the estimated factor and the GDP quarter-on-quarter rate of growth.

Cyclical Analysis
In addition to GDP forecasting, we use the dynamic factor model in other economic studies, including the simulation of macro scenarios and cyclical analysis. For example, we have used the model and cyclical bandpass filters to identify turning points in the business cycle for the past 20 years. Using Signal Processing Toolbox™, we applied a Butterworth filter to extract the signal from the data and pinpoint cyclical turning points (Figure 4). We use a bandpass Butterworth filter because it provides a cleaner picture of economic fluctuations than the Hodrick-Prescott filter, which acts like an implicit high-pass filter that leaks high-frequency noise. The absence of irregular components makes it considerably easier for the algorithms to identify business cycle turning points.
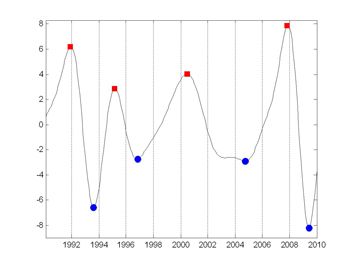
We continue to refine the estimation procedures in the model with MATLAB, and we update the list of indicators as needed to improve the accuracy of our forecasts.
Published 2012 - 92011v00
References
-
Chang-Jin Kim and Charles R. Nelson, State-Space Models with Regime Switching, MIT Press 1999.