Linear regression is a statistical modeling technique used to describe a continuous response variable as a function of one or more predictor variables. It can help you understand and predict the behavior of complex systems or analyze experimental, financial, and biological data.
Linear regression techniques are used to create a linear model. The model describes the relationship between a dependent variable \(y\) (also called the response) as a function of one or more independent variables \(X_i\) (called the predictors). The general equation for a linear regression model is:
\[Y = \beta_0 + \sum \ \beta_k X_k + \epsilon_i\]
where \(\beta\) represents linear parameter estimates to be computed and \(\epsilon\) represents the error terms.
Types of Linear Regression
Simple linear regression (models using only one predictor): The general equation is:
\[Y = \beta_0 + \beta_1 X+ \epsilon\]

Simple linear regression example showing how to predict the number of fatal traffic accidents in a state (response variable, \(Y\)) compared to the population of the state (predictor variable, \(X\).). (See MATLAB® code example and how to use the mldivide operator to estimate the coefficients for a simple linear regression.)
Multiple linear regression (models using multiple predictors): This regression has multiple \(X_i\) to predict the response, \(Y\). An example of this equation is:
\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2+ \epsilon\]
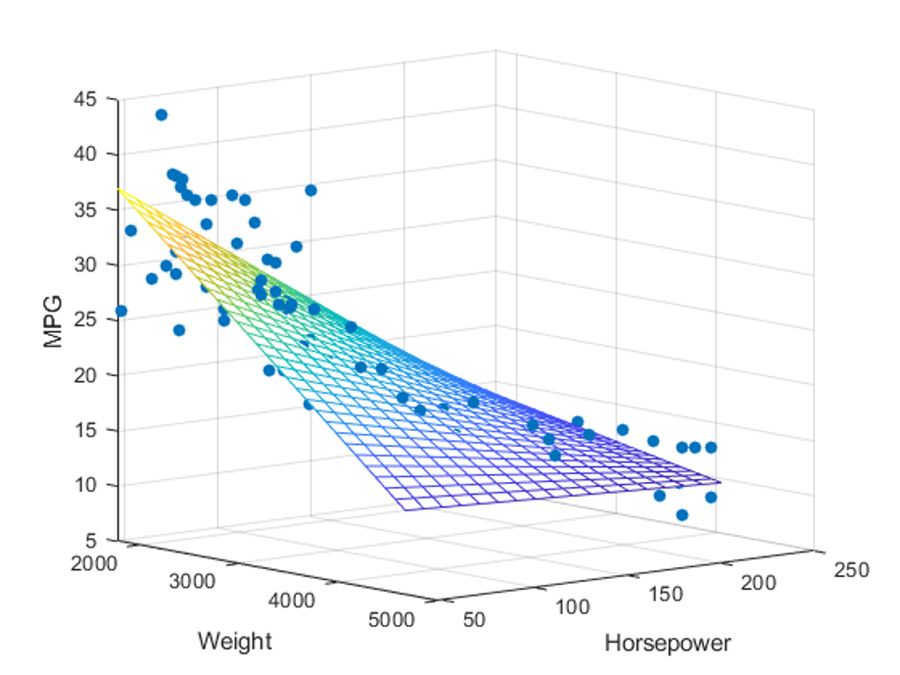
Multiple linear regression example, which predicts the miles per gallon (MPG) of different cars (response variable, \(Y\)) based on weight and horsepower (predictor variables, \(X_j\)). (See MATLAB code example, how to use the regress function and determine significance of the multiple linear regression relationship.)
Multivariate linear regression (models for multiple response variables): This regression has multiple \(Y_i\)derived from the same data \(X\). They are expressed in different formulae. An example of this system with 2 equations is:
\[Y_1 = \beta_{01} + \beta_{11} X_1 + \epsilon_1\]
\[Y_2 = \beta_{02} + \beta_{1 2}X_1 + \epsilon_2\]
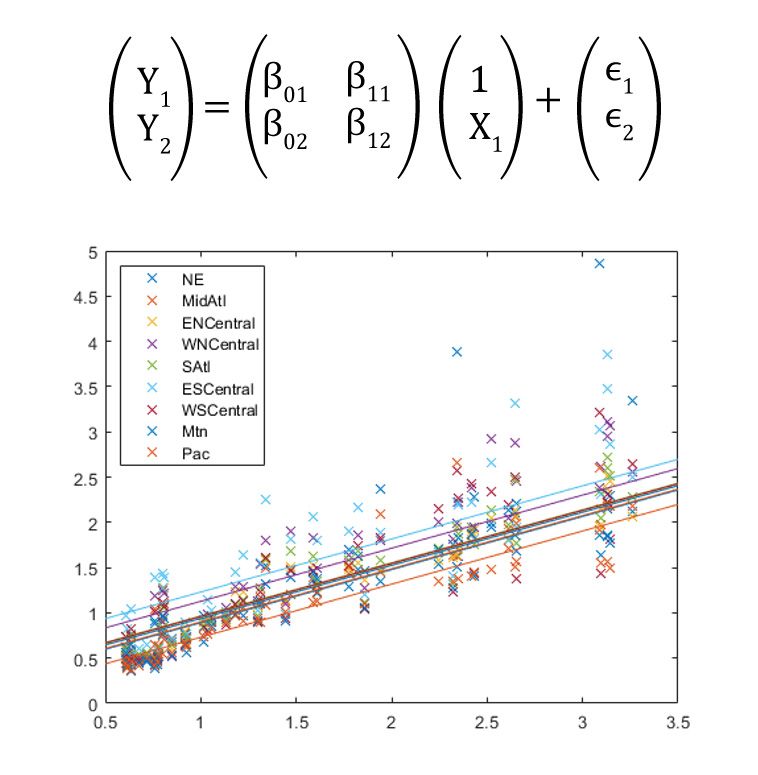
Multivariate linear regression example showing how to predict the flu estimates for 9 regions (response variables, \(Y_i\)), based on the week of the year (predictor variable, \(X\)). (See MATLAB code example and how to use the mvregress function to determine the estimated coefficients for a multivariate linear regression.)
Multivariate multiple linear regression (models using multiple predictors for multiple response variables): This regression has multiple \(X_i\) to predict multiple responses \(Y_i\). A generalization of the equations is:
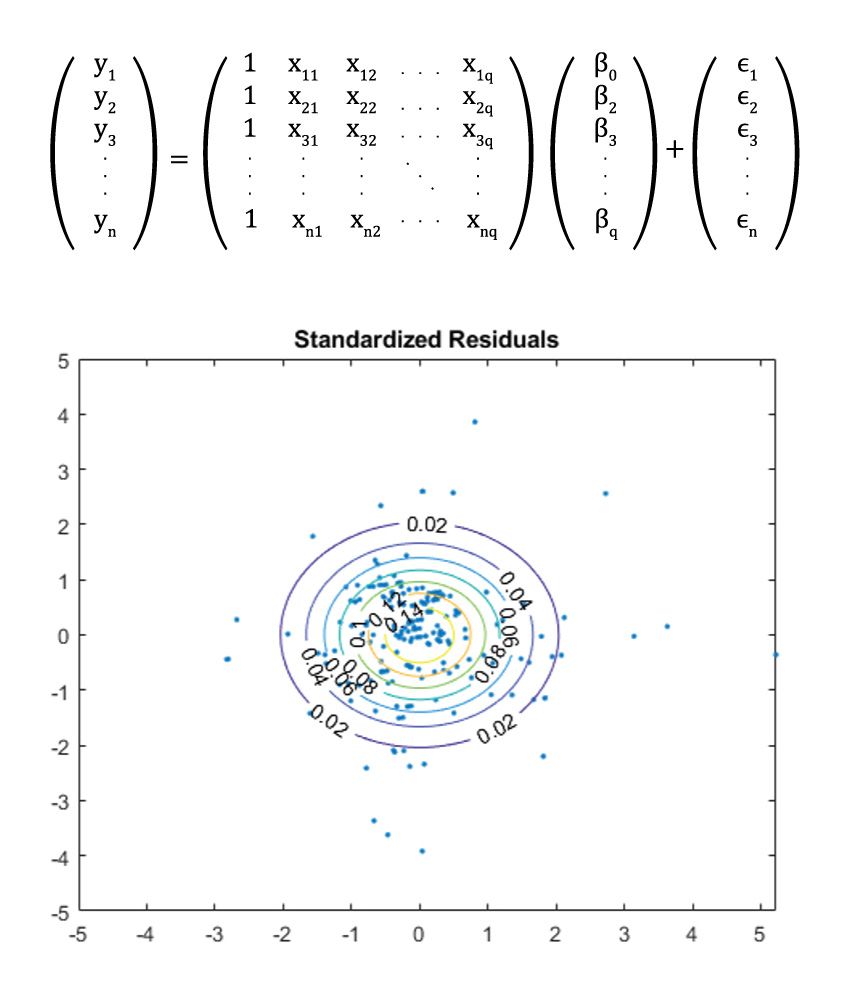
Multivariate multiple linear regression example that calculates the city and highway MPG (as response variables, \(Y_1\) and \(Y_2\)) from three variables: wheel base, curb weight, and fuel type (predictor variables, \(X_1\), \(X_2\) and \(X_3\)). (See MATLAB code example and how to use the mvregress function to estimate the coefficients.).
Applications of linear regression
Linear regressions have some properties that make them very interesting for the following applications:
- Prediction or forecasting: Use a regression model to build a forecast model for a specific data set. From the model, you can use regression to predict response values where only the predictors are known.
- Strength of the regression: Use a regression model to determine if there is a relationship between a variable and a predictor, and how strong this relationship is.
Linear regression with MATLAB
Engineers commonly create simple linear regression models with MATLAB. For multiple and multivariate linear regression, you can use the Statistics and Machine Learning Toolbox™ from MATLAB. It enables stepwise, robust, and multivariate regression to:
- Generate predictions
- Compare linear model fits
- Plot residuals
- Evaluate goodness-of-fit
- Detect outliers
To create a linear model that fits curves and surfaces to your data, see Curve Fitting Toolbox™.
Keep Exploring This Topic
Resources
Expand your knowledge through documentation, examples, videos, and more.
Discover More
- Linear Model Function in Statistics and Machine Learning Toolbox - Function
- Forecast Electrical Load Using the Regression Learner App (3:42) - Video
- Fitting with MATLAB: Statistics, Optimization, and Curve Fitting (38:37) - Video
- MATLAB Tools for Scientists - Introduction to Statistical Analysis (54:52) - Video
- Machine Learning with MATLAB Overview (3:02) - Video

