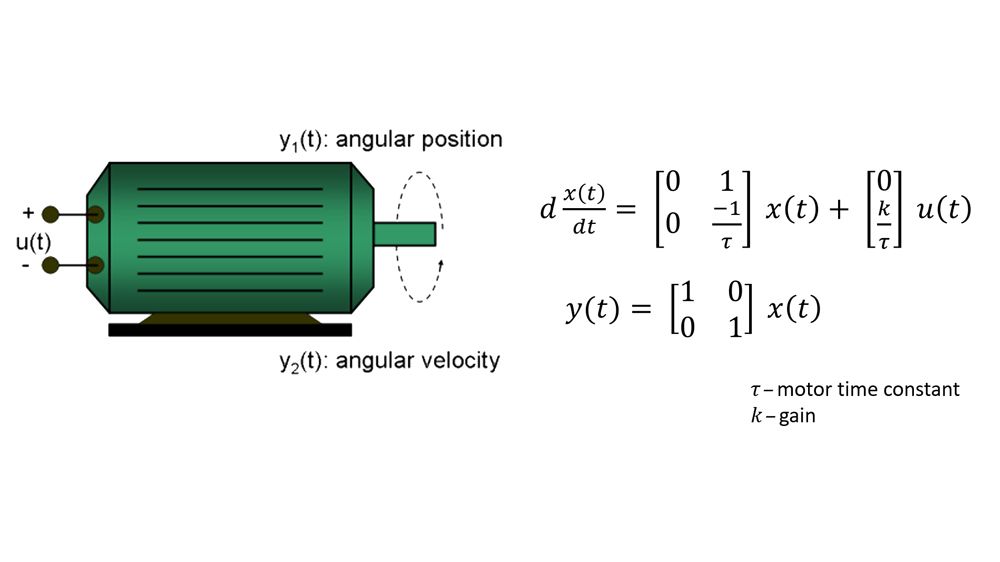
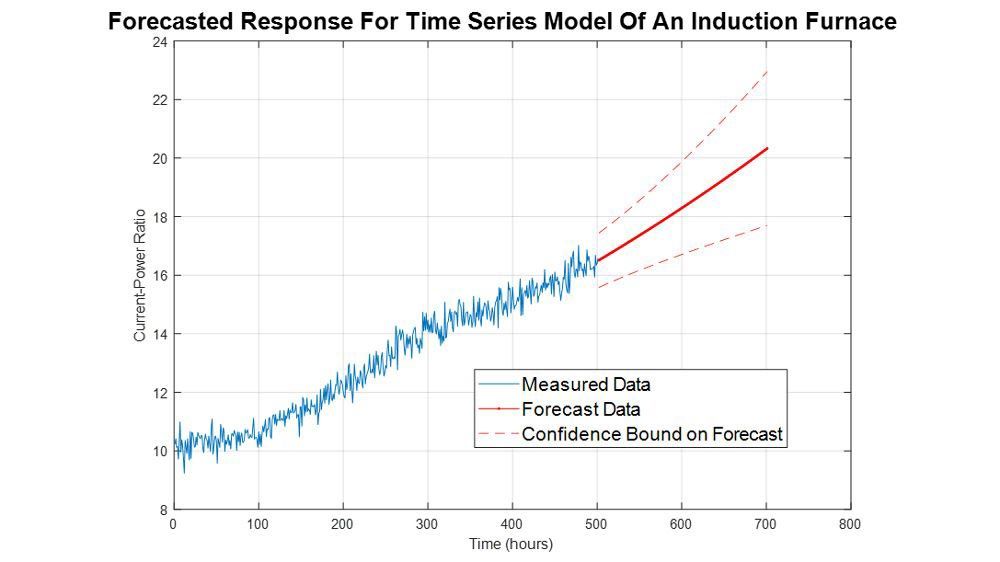
System Identification Toolbox 提供用于动态系统建模、时间序列分析和预测的 MATLAB 函数、Simulink 模块和 App。您可以了解测得变量之间的动态关系,以使用时域或频域数据创建连续或离散时间的传递函数、过程模型和状态空间模型。您可以使用 AR、ARMA 及其他线性和非线性自回归建模方法来预测时间序列。
本工具箱支持您通过 Hammerstein-Wiener 和非线性 ARX 模型使用机器学习方法(如高斯过程 (GP)、支持向量机 (SVM) 和其他表示法)来估计非线性系统动态特性。您也可以使用深度学习来创建神经常微分方程 (ODE) 模型来捕获非线性系统动态特性。本工具箱可让您执行灰箱系统辨识以估计用户定义模型的参数。您可以将辨识的模型集成到 Simulink 中进行快速仿真,以实现控制设计以及诊断和预后应用。
您可以使用扩展或无迹卡尔曼滤波器和粒子滤波器进行在线参数和状态估计,用于自适应控制、故障检测和软测量应用。该工具箱支持您为在线估计算法生成 C/C++ 代码以部署到嵌入式设备。
基于人工智能的非线性系统辨识
将机器学习和深度学习方法与非线性 ARX 和 Hammerstein-Wiener 模型相结合,以描述系统的非线性动态特性。借助 Statistics and Machine Learning Toolbox 和 Deep Learning Toolbox,使用支持向量机 (SVM)、树集成、高斯过程和前馈网络来表示非线性。还可以使用神经 ODE 创建基于深度学习的非线性状态空间模型。
控制系统设计与 Simulink
使用您估计的模型作为被控对象模型通过 Control System Toolbox 设计和调节控制器。在 Simulink 中使用内置模块实现估计的模型、状态估计器和递归模型,用于系统分析、虚拟传感器建模、降阶建模和控制设计。
部署
使用代码生成为在线故障检测、降阶建模 (ROM) 以及诊断和预测等应用部署估计的模型、状态估计器和递归模型。分别使用 Simulink Coder 和 Simulink PLC Coder 为在 Simulink 中实现的模型生成 C/C++ 代码和 IEC 61131-3 结构化文本。使用 MATLAB Coder 在 MATLAB 中生成 C/C++ 代码。或者,使用 MATLAB Compiler 生成独立应用。
产品资源:
“通过使用 Optimization Toolbox 和 System Identification Toolbox 改进我们现有的 AFR 控制系统的性能,我们显著减少了废气的产生。在对我们正在开发的发动机进行评估时,我们发现在某些条件下 NOx 和 CO 排放至少减少了一半。”
Hiroshi Katoh,日产汽车公司