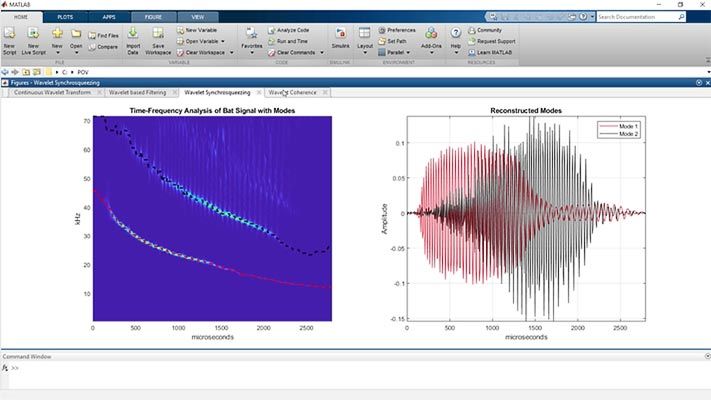
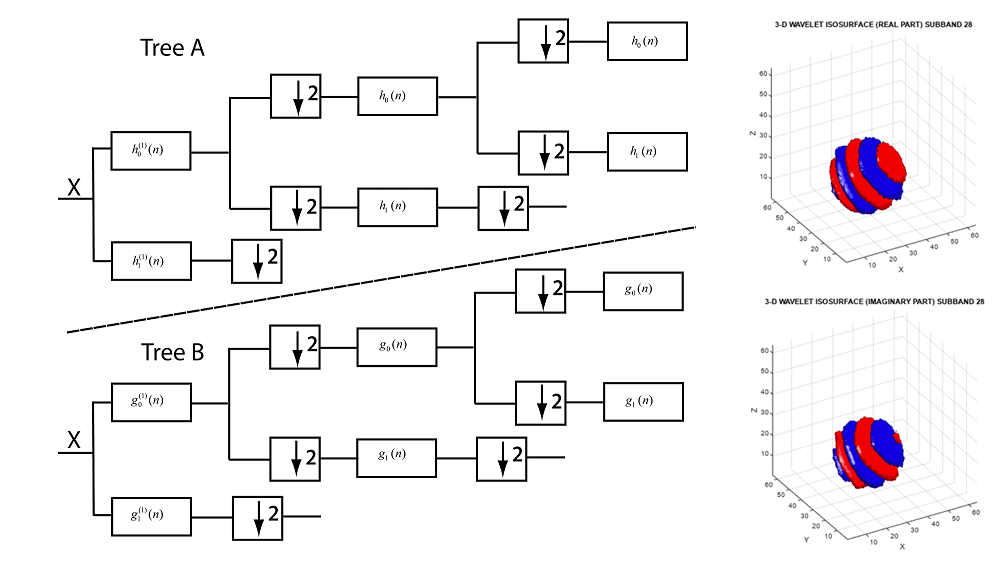
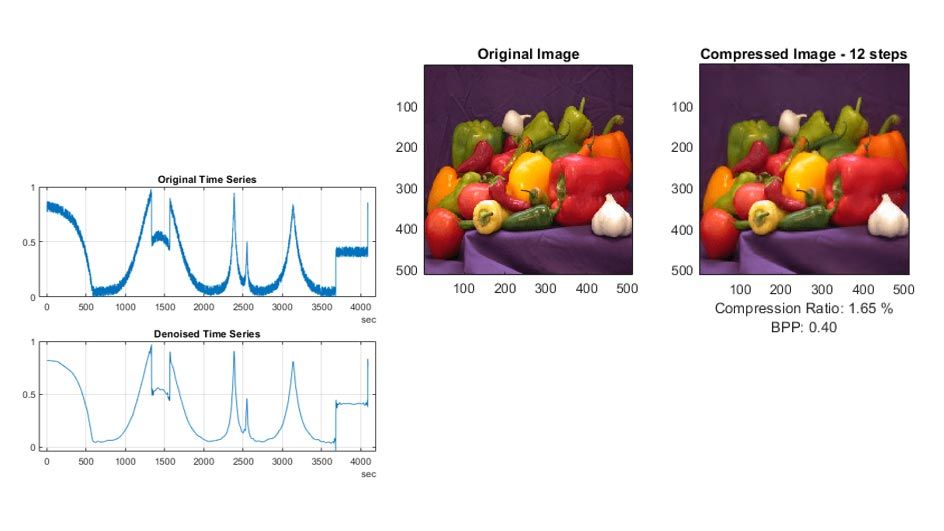
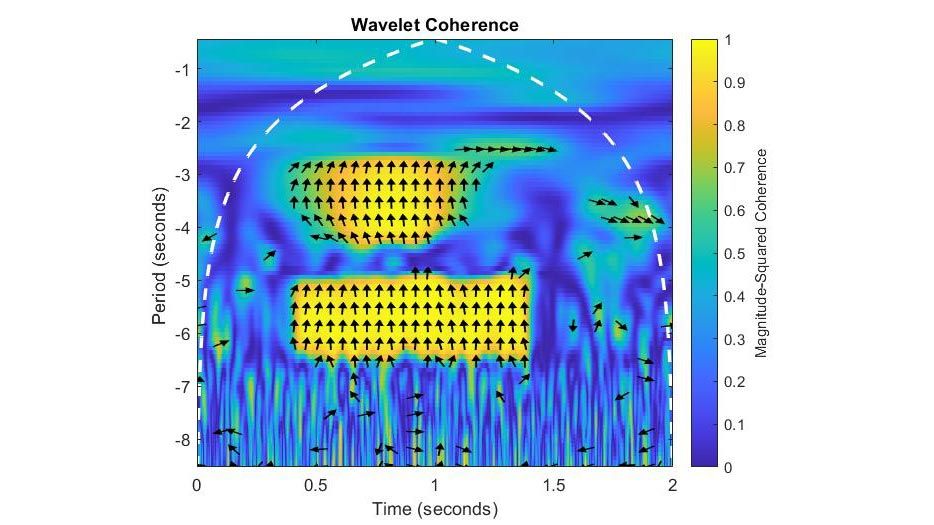
Wavelet Toolbox 为信号的时频分析和图像的多尺度分析提供 App 和函数。您可以对数据进行去噪和压缩,并检测异常、变化点和瞬变。该工具箱通过提供时频变换和自动特征提取,包括散射变换、连续小波变换(尺度图)、Wigner-Ville 分布和经验模态分解,来支持以数据为中心的人工智能 (AI) 工作流。您可以使用小波、小波包和剪切波变换从图像中提取边缘和方向特征。
这些 App 支持您以交互方式执行时频分析、信号去噪或图像分析,并生成 MATLAB 脚本来重现或自动化您的工作。
您可以从工具箱函数中生成 C/C++ 和 CUDA® 代码以用于嵌入式部署。
加速和部署
使用 GPU 和多核处理器运行支持的函数,从而加快代码执行速度。对于支持 C/C++ 代码生成的 Wavelet Toolbox 函数,可使用 MATLAB Coder 为其生成独立的 ANSI 兼容 C/C++ 代码。为支持的函数生成优化 CUDA 代码以在 NVIDIA® GPU 上运行。